С.В. Богуславский, В.П. Литвинов
ООО «БМГ-Кварц», Московский государственный открытый университет
ВВЕДЕНИЕ
В настоящее время существует значительное количество учебников, методических пособий и научных статей для расчета кварцевых генераторов. Однако им присущ один серьезный недостаток: все они в той или иной мере оторваны от практического применения за счет наличия большого числа математических выражений, изобилующих комплексными выражениями, дифференциальными уравнениями и системами и т.д.
Но самое главное, решение все равно требует дополнительной коррекции при практической реализации, т.к. при расчете нелегко учесть разброс параметров элементов схемы, да и в справочниках приведены далеко не все необходимые параметры. В результате усилия, затраченные на расчет схемы, зачастую бывают сведены «на нет» при практической реализации.
Целью настоящей и последующих работ является создание такой инженерной методики расчета кварцевых генераторов различных типов схем, при которой можно в короткие сроки произвести расчет генератора, имея под рукой всего лишь инженерный калькулятор.
Предлагаемая методика предназначена для разработчиков радиоаппаратуры, имеющих некоторый практический опыт разработки аналоговых электронных схем, в частности автогенераторов или кварцевых генераторов, поэтому расчетные формулы приведены без выводов.
Кроме того, в другой статье предложена методика более углубленного анализа кварцевых генераторов после ее инженерного расчета с использованием САПР Micro Cap.
1. Эквивалентная электрическая схема кварцевого резонатора.
Основным элементом схемы генератора, определяющим его стабильность является кварцевый резонатор, эквивалентная электрическая схема которого приведена на рис.1.
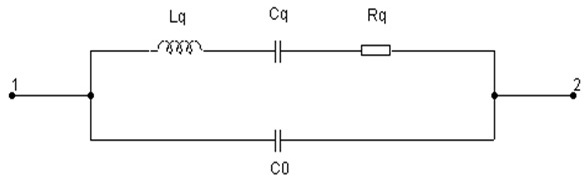
Рис.1. Эквивалентная схема кварцевого резонатора
Поясним физический смысл электрических параметров эквивалентной схемы кварцевого резонатора:
- Lq – эквивалентная динамическая индуктивность – эквивалент колеблющейся массы под электродами резонатора, величина которой определяет величину добротности Q;
- Cq – эквивалентная динамическая емкость – эквивалент механической жесткости кварцевой пластины;
- Rq – эквивалентное динамическое сопротивление – величина, характеризующая активные потери в кристаллической решетке, демпфирование колебаний молекулами окружающего газа и электрические потери в подводящих электродах;
- C0 – статическая емкость кварцедержателя.
Для диапазона частот от 5 до 30 МГц типовые значения элементов эквивалентной схемы следующие: Cq=0.008…0.02 пФ; Lq=5…30 мГн; Rq=5…50 Ом; C0=1,5…6 пФ.
При проектировании генераторов, работающих на частотах выше 30 МГц применяют кварцевые резонаторы, работающие на нечетных механических гармониках (3-я, 5-я, 7-я и т.д.). При этом значения Cq уменьшаются пропорционально квадрату номера гармоники, т.е. на 3-ей механической гармонике резонатор будет иметь Cq порядка 0,01/32≈0,001 пФ. При этом эквивалентное сопротивление возрастает приблизительно прямо пропорционально номеру гармоники, т.е. 3xRq.
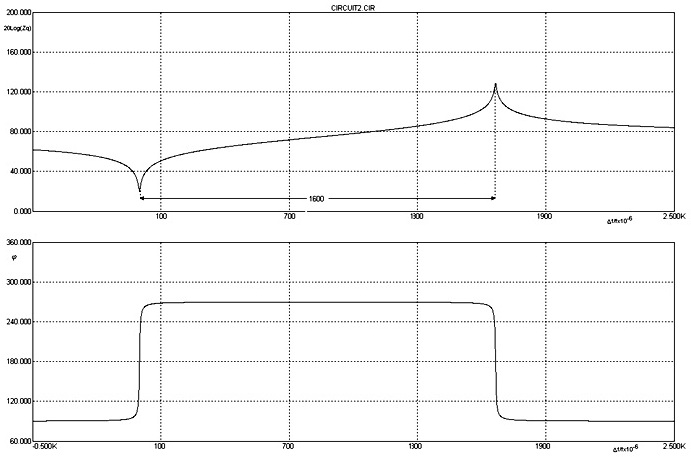
Как видно из рис. 1, эквивалентная схема представляет собой сложный колебательный контур, имеющий последовательный и параллельный резонанс, причем частота последовательного резонанса определяется параметрами Lq и Cq, а параллельного – Lq и последовательно соединенных Cq и C0. Наличие резонансов иллюстрирует рис. 2, на котором приведены амплитудно-частотная (АЧХ) и фазо-частотная (ФЧХ) характеристики полного сопротивления Zq кварцевого резонатора частотой 10 МГц по 1-ой механической гармонике.
Рис.2. Характеристики полного сопротивления резонатора.
Из рисунка видно, что частотная характеристика имеет два экстремума, соответствующих последовательному (минимум) и параллельному (максимум) резонансу.
Разность частот между ними называется резонансным промежутком, который можно определить как

Особый интерес представляет область АЧХ между последовательным и параллельным резонансом, характеризующаяся увеличением полного сопротивления с ростом частоты, что соответствует индуктивному характеру сопротивления резонатора, величина которого зависит от отстройки от частоты последовательного резонанса.
2. Условие самовозбуждения генератора
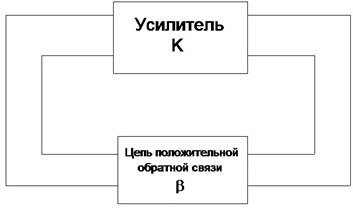
В самом общем виде структурную схему автогенератора (рис. 3) можно представить состоящей из двух четырехполюсников – усилителя с коэффициентом усиления K и цепи положительной обратной связи с коэффициентом обратной связи β.
Рис. 3. Структурная схема автогенератора.
Условие стационарного режима генератора можно представить в следующем виде:
![]()
Выражение (2) состоит из двух уравнений – баланса фаз и баланса амплитуд.
Баланс фаз – алгебраическая сумма сдвигов фаз по замкнутому колебательному контуру равна 0 или 2πn.
Баланс амплитуд – условие, при котором в установившемся режиме произведение коэффициента усиления активной части схемы (усилителя) на коэффициент обратной связи, называемое фактором регенерации G, равно 1. Для уверенного возбуждения генератора начальное значение G выбирается в пределах от 2 до 4. При установлении колебаний величина G снижается до 1 – выполнения условия баланса амплитуд, за счет уменьшения средней крутизны при росте амплитуды колебаний.
3. Осцилляторные схемы кварцевых генераторов.
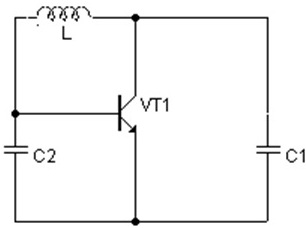
В технике стабилизации частоты, наиболее часто используют так называемые осцилляторные схемы, т.е. схемы, в которых кварцевый резонатор является элементом колебательного контура генератора – как правило, индуктивностью. Эти генераторы выполняются обычно по схеме «емкостной трехточки» (Рис.3.),
Рис.3.1. Обобщенная схема емкостной трехточки.
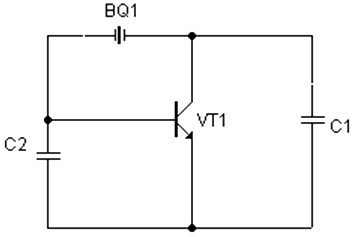
В зависимости от того, какой электрод транзистора VT1 будет заземлен, схема будет называться с общей базой, с общим эмиттером или с общим коллектором. Как было уже сказано выше, индуктивность в этой схеме можно заменить кварцевым резонатором. При этом рабочая частота генератора будет выше частоты последовательного резонанса кварцевого резонатора. Схема кварцевого генератора, построенного по схеме емкостной трехточки, будет иметь вид, показанный на рис.4.
Рис.4. Обобщенная схема кварцевого генератора
4. Методика расчета кварцевого генератора
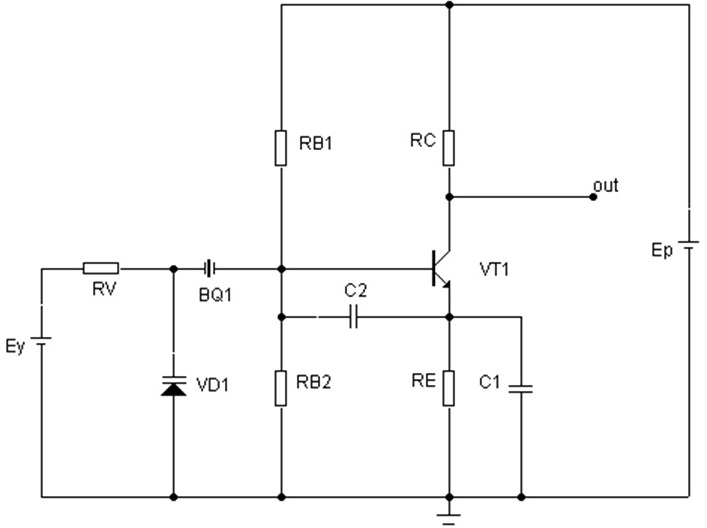
В качестве примера проведем анализ и расчет, наиболее распространенной схемы управляемого напряжением кварцевого генератора (рис.5.), которая практически применяется в большей части радиотехнических устройств,. В ней RB1 и RB2 — сопротивления базового делителя, RC – коллекторная нагрузка, RE – резистор в цепи эмиттера, C1, C2, BQ1 и VD1 – элементы контура генератора и RV – резистор цепи управления варикапа. Варикап RV может использоваться также для подстройки частоты в неуправляемом генераторе, расчет которого производится аналогичным образом.
Рис.5. Принципиальная схема управляемого кварцевого генератора.
Анализ и расчет работы генератора целесообразно начать с расчета режима работы по постоянному току. Для этого совсем необязательно иметь весь набор параметров и характеристик транзистора. Дело в том, что современные кремниевые транзисторы, используемые в качестве активного элемента кварцевых генераторов, как правило, имеют коэффициент усиления по току β≥100, а частоту единичного усиления ft ≥ 1500…2000 МГц, что позволяет пренебречь инерционными свойствами транзистора вплоть до частот порядка 100 МГц.
Прежде всего, найдем значение тока коллектора в рабочей точке. Так как напряжение перехода база-эмиттер транзистора в открытом состоянии составляет 0,6…0,75 В, ток коллектора (без учета тока базы) определяется по формуле:

Далее, находим крутизну вольтамперной характеристики:

где ![]() — температурный потенциал;
— температурный потенциал;
k – постоянная Больцмана;
T – абсолютная температура;
q – заряд электрона.
Затем, определяем управляющее сопротивление Ry, равное произведению сопротивления нагрузки на коэффициент обратной связи резонансной цепи генератора:

где
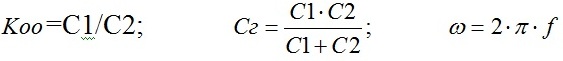
Для проверки условия баланса амплитуд определяем фактор регенерации G:
![]()
Определение значения рабочей частоты генерации включает в себя:
- определение емкости варикапа при среднем значении напряжения перестройки;
- определение емкости генератора;
- расчет частоты генерации при различных напряжениях перестройки.
В перестраиваемых генераторах для получения больших пределов перестройки частоты и хорошей линейности ее характеристики обычно применяют варикапы со сверхрезким переходом. Аналитическая зависимость емкости варикапа от напряжения обратного смещения аппроксимируется следующим образом:

где Cv0- емкость варикапа при напряжении управления Ey=0.
Относительная отстройка от частоты последовательного резонанса

где 1/ =1/С1+1/С2+1/ .
Рабочая частота генератора 
После этого приступаем к анализу энергетических характеристик генератора.
Из анализа спектральной характеристики коллекторного тока известно, что амплитуда первой гармоники коллекторного тока Icm при G≥3 равна 2lc. Поэтому амплитуда переменного напряжения база-эмиттер Ube=Icm x Ry .
Ток, протекающий в контуре генератора, а также через кварцевый резонатор можно определить из следующего выражения:
![]()
Мощность, рассеиваемая на кварцевом резонаторе определяется как
![]()
Амплитуда первой гармоники выходного напряжения генератора равна
![]()
5. Пример расчета кварцевого генератора
В качестве примера рассчитаем кварцевый генератор, управляемый напряжением со следующими параметрами:
• Номинальная частота ,ƒ0 10 МГц;
• Перестройка частоты, δ ±100×10-10;
• Диапазон изменения напряжения управления, Ey 0…5 В;
• Амплитуда 1-ой гармоники выходного напряжения, Ucm≥250мВ;
• Сопротивление коллекторной нагрузки, Rc 200 Ом;
• Напряжение питания, Ep 5В≥10%.
Кварцевый резонатор берем со следующими типовыми параметрами:
Номинальная частота 10 МГц;
Динамическое сопротивление 10 Ом;
Динамическая емкость 10 фФ;
Статическая емкость 3 пФ.
1. По формуле (3) определяем ток коллектора в рабочей точке
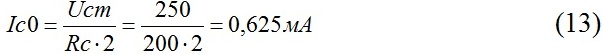
2. Крутизна коллекторного тока согласно формуле (4) будет равна
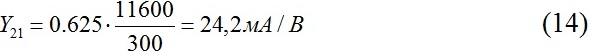
3. Для обеспечения широкого диапазона перестройки частоты генератора задаемся фактором регенерации G=5 и определяем управляющее сопротивление Ry
![]()
4. Определяем эквивалентную емкость генератора

Если С1=С2 то С1=С2=347х2=794 пФ. Из ряда Е24 выбираем ближайшие значения емкостей конденсаторов С1=С2=750 пФ
5. Определяем элементы схемы генератора, задающие режим по постоянному току.
Выбираем 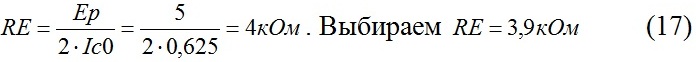
6. Определяем элементы цепи базового смещения
Выбираем ток делителя . 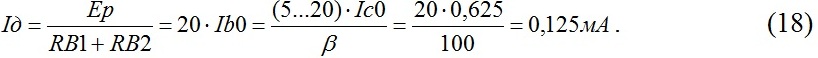
Напряжение на базе транзистора , 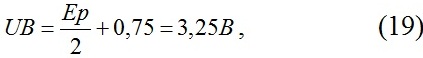
![]()
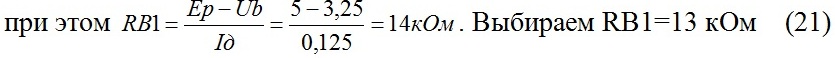
7. Для определения перестройки частоты из выражения (8) находим
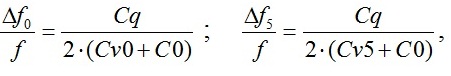
тогда общая перестройка будет равна
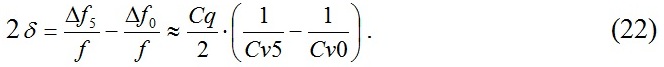
Умножая левую и правую части равенства на получаем
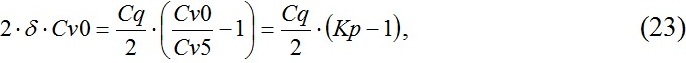
где Kp – коэффициент перекрытия варикапа по емкости.
Выбрав Kp=3 определим .
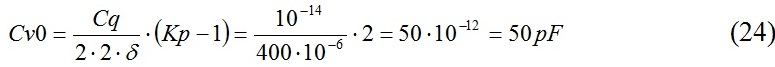
При этом 
Выбираем варикап BB659, у которого =55 pF, а =18 pF.
8. В заключение определим также мощность рассеяния на кварцевом резонаторе
![]()
Подставляя в данное выражение значения параметров, получаем:
![]()
Допустимая мощность для данного типа резонаторов составляет 1 mW или 1000μW .
_______________________________________________________________________________________